Part 1. Overview of Metamorphism and Tectonics
Part 2. Introduction to Metamorphism
Part 3. Physical Processes of Metamorphism
Part 4. Introductory Phase Equilibria and Thermodynamics
Part 5. Ultramafic Rocks
Part 6. Mafic Rocks
Part 7. Pelitic Rocks
Part 8. Diffusion
Part 9. Thermobarometry
Part 10. Kinetics
Part 11. Interaction Between Metamorphism and Deformation
Part 12. Metamorphism and Geochronology
Part 13. Metamorphism and Tectonics I
Part 14. Metamorphism and Tectonics II
Thermodynamics Notes
Part 9. Thermobarometry
Read pages 53-70 of Vernon and Clarke or Chapter 16 of I&M Petrology by Best
or Chapter 27 of Igneous and Metamorphic Petrology by John Winter
or Chapter 19 of Igneous and Metamorphic Petrology by Philpotts
Pressure-Temperature Paths
One of the important goals of metamorphic petrologists is to reconstruct the P-T paths experienced by rocks. In general, this goal is attained by textural analysis combined with thermobarometry.
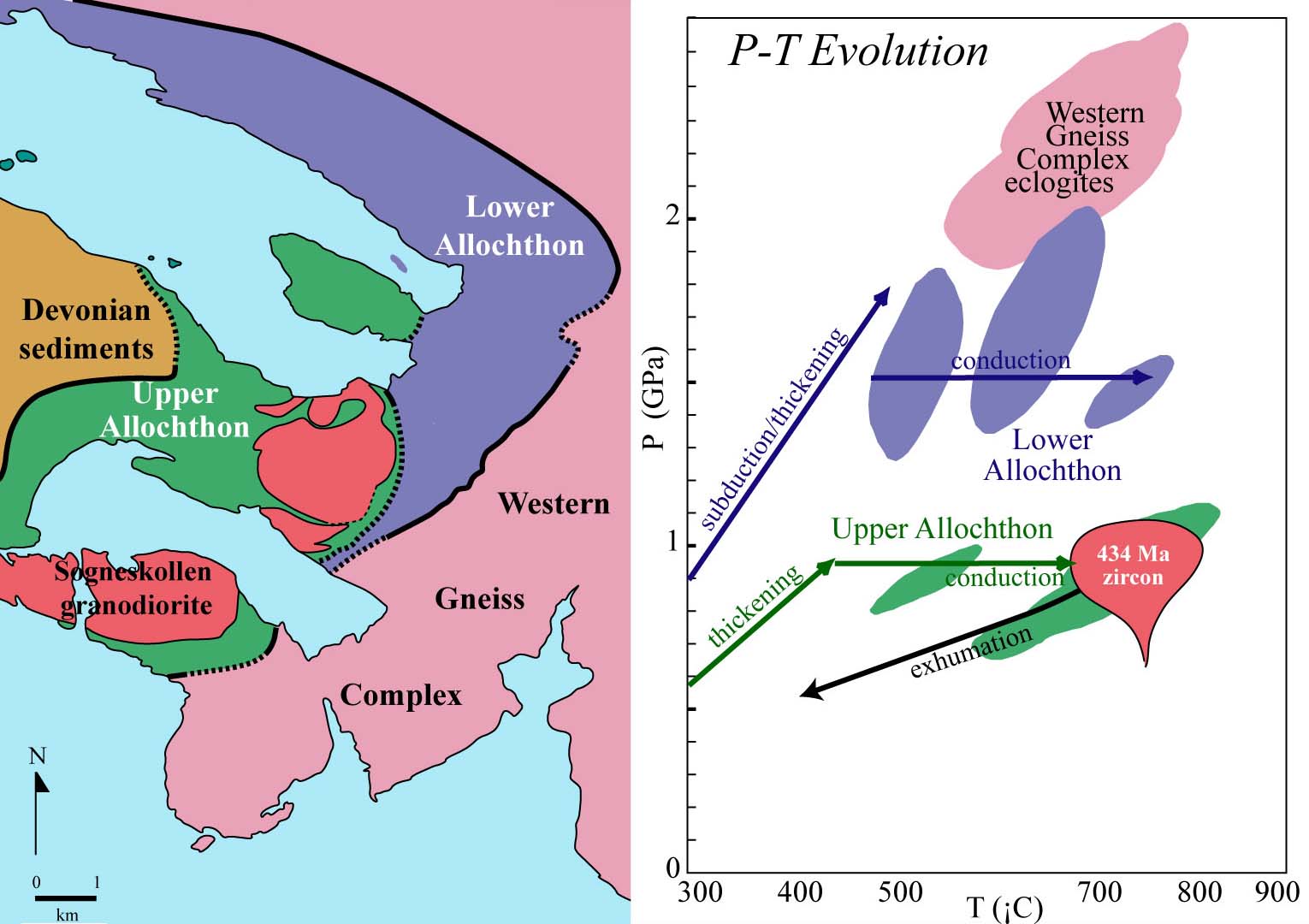
peak temperature: the maximum T experienced by a rock
peak pressure: the maximum P experienced by a rock
metamorphic field gradient: a spatially varying sequence of peak pressures
and temperatures.
Qualitative thermobarometry can be done simply by inspection of rocks and minerals
in the field and in thin section, based on reaction textures and mineral assemblages.
These garnets show thin rims of plagioclase, likely related to decompression:

Quantitative Thermobarometry
More sophisticated, quantitative determination of metamorphic pressures and temperatures involves four steps:
- careful assessment of reaction textures
- identification of zoning
- measurement of mineral compositions
- application of thermodynamics.
Mineral compositions can be measured with an electron microprobe to high accuracy; they can be measured to lower detection limits with an ICP mass spectrometer.

- Assessment of reaction textures. The purpose of this step is to identify
which minerals are early, which are late, and which are part of a stable
assemblage. Early minerals are likely to be inclusions or broken, late minerals
may be in cracks or strain shadows, and minerals that are in textural equilibrium
should not be separated by reaction zones. Back-scattered electron imaging
is often a convenient and powerful way to study textures:
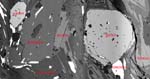
This back-scattered electron image shows zoning in titanite from a Norwegian
gneiss:

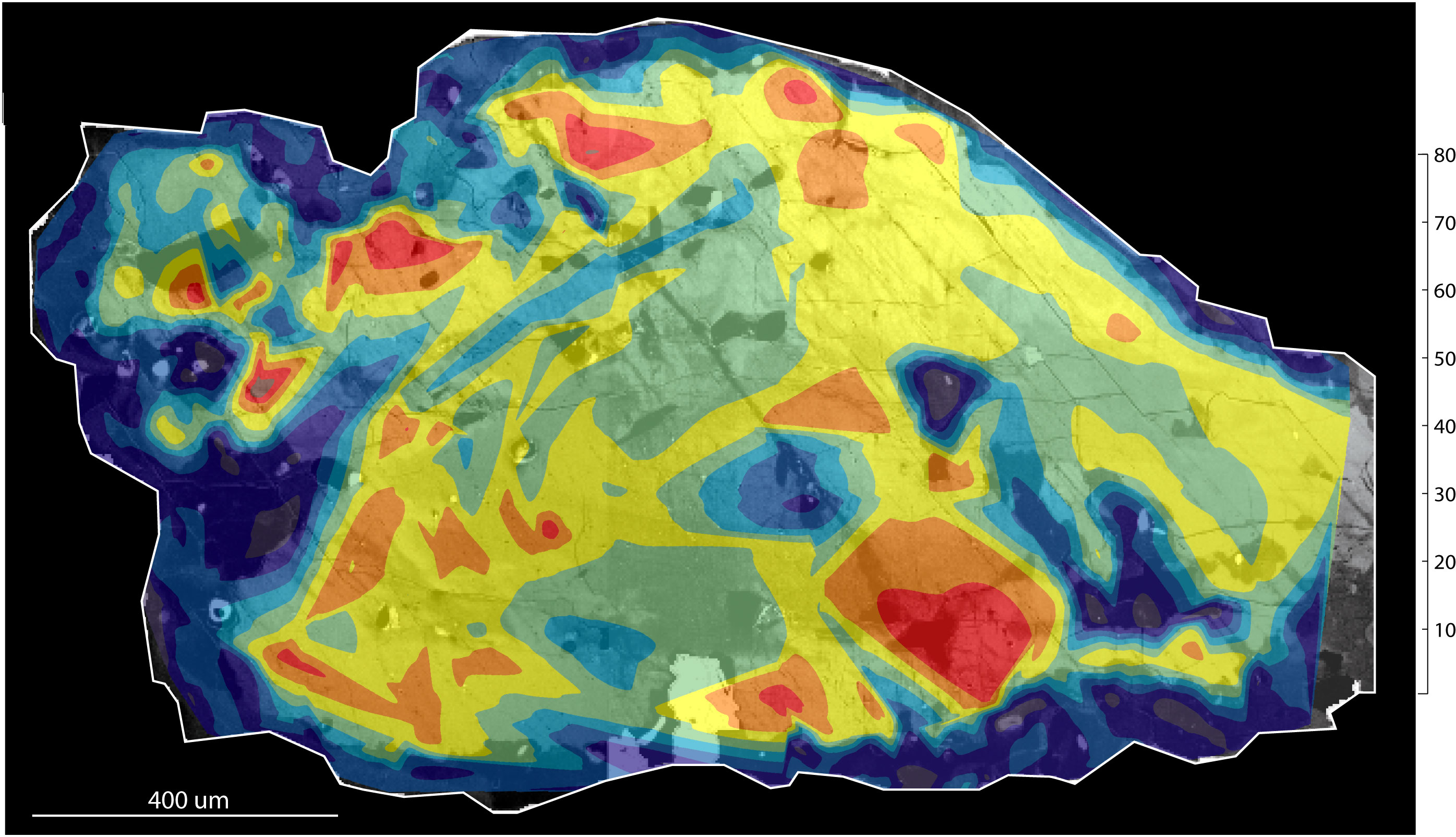
- Identification of zoning. Compositional zoning in minerals can be done
by tuning the electron microprobe spectrometers--or focusing the ICP mass spectrometer detectors--to specific elements and then making element maps:

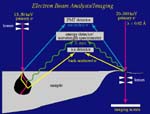
An electron microprobe works by measuring element-characteristic x-rays
emitted by a sample being bombarded with electrons on a 2-micron spot:
Zoning can be quantified over an entire grain with good coverage of spot
analyses:

Such zoning can quantified using line scanning:

- Application of thermodynamics. Experiments have been used to determine
the PT positions of many different kinds of endmember reactions.
For example, experiments have shown that the distribution of Fe and Mg between
garnet and biotite is a function of inverse temperature:

thermometry: The assessment of metamorphic temperatures.
Quantitative thermometry typically is based on the exchange of Fe and
Mg between pairs of minerals. For example, the exchange of Fe and Mg between
garnet and biotite can be written as a reaction among the Fe and Mg endmembers
of these minerals:
- Fe3Al2Si3O12 + KMg3AlSi3O10(OH)2
= Mg3Al2Si3O12 + KFe3AlSi3O10(OH)2

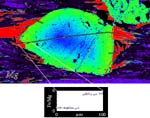
barometry: The assessment of metamorphic pressures.
Qualitative barometry is based on mineral assemblages-such as the coexistence
of kyanite + staurolite.
Quantitative barometry typically is based on net transfer reactions
For example, garnet - aluminumsilicate - silica - plagioclase (GASP)
- 3CaAl2Si2O8 = Ca3Al2Si3O12
+ 2Al2SiO5 + SiO2
- 3 anorthite = grossular + 2 kyanite + quartz

Examples of P-T Determinations
Let's look at some examples of quantitative determinations of metamorphic pressures and temperatures.
Pressures and temperatures of equilibration in lower crustal xenoliths from Tibet were constrained using
compositions of garnet, pyroxene, and plagioclase.

The Fe-Mg garnet-cpx reaction is
- almandine + diopside = pyrope + ferrosilite.
One Al-garnet-opx reaction is
- CaMgSi2O6 diopside + CaAl2SiO6 'cats' = Ca2MgAl2Si3O12 garnet or
- CaFeSi2O6 hedenbergite + CaAl2SiO6 'cats' = Ca2FeAl2Si3O12 garnet
The GOPS reaction is
- grossular + 2 pyrope + 3 quartz = 3 enstatite + 3 anorthite or
- grossular + 2 almandine + 3 quartz = 3 ferrosilite + 3 anorthite.
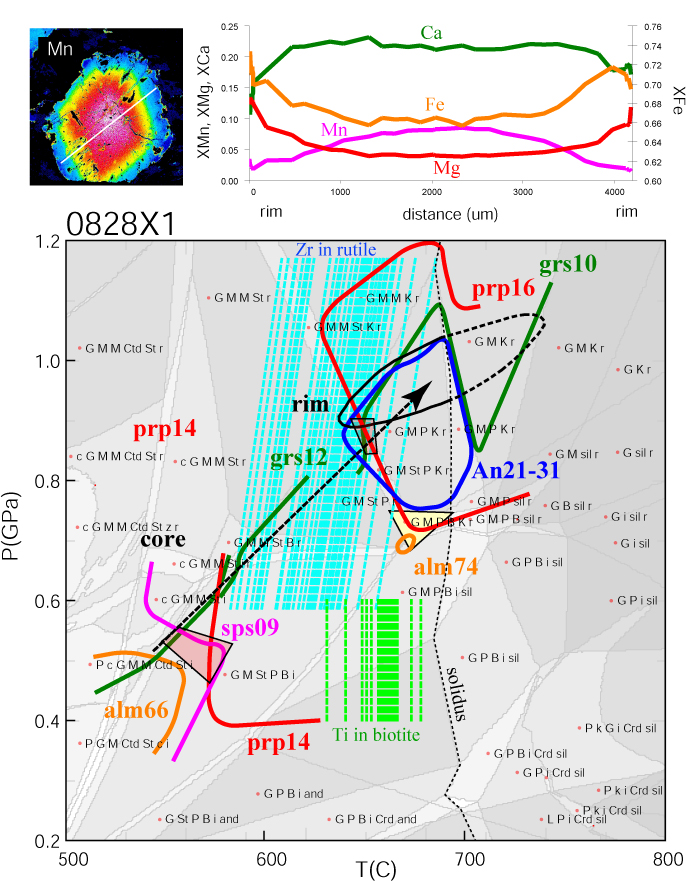
A Detailed Example
Here is an example, using a rock from the Pamir of Tajikistan, of the result of an integrated approach to thermobarometry that uses
phase-stability fields, exchange thermometry, net-transfer reactions, and garnet zoning to determine a P-T history.
Quantitative Geothermometry and Geobarometry
Quantitative thermometry and barometry are based on thermodynamics.
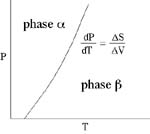
Clapeyron Relation
There is a useful relation between the slope of a reaction in PT space (i.e.,
dP/dT) and the entropy and volume changes of the reaction that follows from
At equilibrium  G = 0, such that
G = 0, such that
 rVdP =
rVdP =  rSdT
rSdT
or
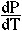 =
= 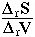
So, the P-T slope of a reaction is equal to the ratio of the entropy change
to the volume change. Alternatively, along the equilibrium curve, the changes
in pressure times the volume change are equal to changes in temperature times
the entropy change. This is the Clapeyron Equation.
Popular thermometers include garnet-biotite (GARB), garnet-clinopyroxene,
garnet-hornblende, and clinopyroxene-orthopyroxene; all of these are based
on the exchange of Fe and Mg, and are excellent thermometers because  rV
is small, such that
rV
is small, such that
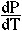 =
= 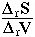
is large (i.e., the reactions have steep slopes and are little influenced by
pressure). In contrast, as we will see, reactions with gentle slopes are the
best barometers.
Calculating the PT Position of a Reaction
Because  rG = 0 at equilibrium, we can write
the following approximation (ignoring fluids and variable heat capacities): rG = 0 at equilibrium, we can write
the following approximation (ignoring fluids and variable heat capacities):
- 0 =
 rH1,Tref - T rH1,Tref - T rS1,Tref
+ rS1,Tref
+  rVsP rVsP
and thus we can calculate the pressure of a reaction at different temperatures
by
- P =
  rH1,Tref
- T rH1,Tref
- T rS1,Tref rS1,Tref![]().jpg) / -
/ - rVs rVs
and we can calculate the temperature of a reaction at different pressures by
- T = Tref +
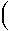  rH1,Tref
+ rH1,Tref
+  rVsP rVsP![]().jpg) /
/  rS1,Tref rS1,Tref
Let's do this for the albite = jadeite + quartz reaction at T = 400 K and T
= 1000 K:
- P = (15,860 - 5147 * 1000) / -1.7342 = 20.6 kbar
Assuming that dP/dT is constant (incorrect in detail), the reaction looks like
this

This is fine and dandy for determining P and T based on the appearance and
disappearance of minerals, but how do we determine P and T based on changes
in mineral composition?
|
Equilibrium Constant
For the reaction
we write the equilibrium constant:
Moreover,
 rG° = -RT ln K
rG° = -RT ln K
or
- ln K = -
 rG°/RT
rG°/RT
At equilibrium, where  rG°= 0, ln
K = 0 and K = 1. This enables us to write a very important relationship:
rG°= 0, ln
K = 0 and K = 1. This enables us to write a very important relationship:
- ln K = - (
 rH1,Tref
- T
rH1,Tref
- T rSTref +
rSTref +  rVsP)/
RT
rVsP)/
RT
Let's see what K looks like for jadeite + quartz = albite at 800 K and 20
kbar:
- = -(15,860 - 800 * 51.47 + 1.7342 * 20,000)/(8.314*800) = -1.4
If we do this for all of PT space, we can contour PT space in terms of lnK:

Solid Solutions
Almost no phases are pure, but typically are mixtures of components. For example,
olivine varies from pure forsterite Mg2SiO4 to pure fayalite
Fe2SiO4, and can have any composition in between--it is
a solid solution. We need a way to calculate the thermodynamic properties
of such solutions.
As a measure of convenience, we use mole fraction to describe the compositions
of phases that are solid solutions. For example, a mix of 1 part forsterite
and 3 parts fayalite yields an olivine with 25 mol% forsterite and 75 mol% fayalite,
which can be written as (Mg0.25Fe0.75)2SiO4
or fo25fa75, etc. Mole fractions are denoted as Xi.
Activity Models (Activity-Composition Relations)
Garnets are solid solutions of
| component |
abbrev. |
formula |
| pyrope |
prp |
Mg3Al2Si3O12 |
| almandine |
alm |
Fe3Al2Si3O12 |
| grossular |
grs |
Ca3Al2Si3O12 |
| spessartine |
sps |
Mn3Al2Si3O12 |
| andradite |
and |
Ca3Fe23+Si3O12 |
The simplest type of useful activity model is the ionic model, wherein we assume
that mixing occurs on crystallographic sites. For a Mg-Fe-Ca-Mn garnet with
mixing on one site, which we can idealize as (A,B,C,D)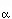 Al2Si3O12,
the activities are Al2Si3O12,
the activities are
- aprp =
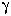 Mg3XMg3 Mg3XMg3
- aalm =
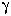 Fe3XFe3 Fe3XFe3
- agrs =
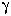 Ca3XCa3 Ca3XCa3
- asps =
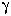 Mn3XMn3 Mn3XMn3
In general, for ideal mixing in a mineral with a single crystallographic site
that can contain 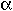 ions, ions,
- ai = Xj
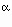
where a, the activity of component i, is the mole fraction of element j raised
to the 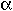 power. power.
Exchange Reactions
Many thermometers are based on exchange reactions, which are reactions
that exchange elements but preserve reactant and product phases. For example:
|
+ KMg3AlSi3O10(OH)2 |
= Mg3Al2Si3O12 |
+ KFe3AlSi3O10(OH)2 |
|
+ phlogopite |
= pyrope |
+ annite |
We can reduce this reaction to a simple exchange vector:
- (FeMg)gar+1 = (FeMg)bio-1
|
Let's write the equilibrium constant for the GARB exchange reaction
- K = (aprpaann)/(aalmaphl)
thus
 rG = -RT ln (aprpaann)/(aalmaphl) rG = -RT ln (aprpaann)/(aalmaphl)
This equation implies that the activities of the Fe and Mg components of biotite
and garnet are a function of Gibbs free energy change and thus are functions
of pressure and temperature.
If we assume ideal behavior (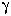 = 1) in garnet and biotite
and assume that there is mixing on only 1 site = 1) in garnet and biotite
and assume that there is mixing on only 1 site
- aalm = Xalm3 = [Fe/(Fe + Mg + Ca + Mn)]3
- aprp = Xprp3 = [Mg/(Fe + Mg)]3
- aann = Xann3 = [Fe/(Fe + Mg)]3
- aphl = Xphl3 = [Mg/(Fe + Mg)]3
Thus the equilibrium constant is
- K = (XMggar XFebio)/(XFegar
XMgbio)
|
- or K = (Xprp3 Xann3)/(Xalm3
Xphl3)
Long before most of you were playground bullies (1978) a couple of deities named
John Ferry and Frank Spear measured experimentally the distribution of Fe and
Mg between biotite and garnet at 2 kbar and found the following relationship:

If you compare their empirical equation
this immediately reminds you of
- ln K = - (
 rG° / RT) = -( rG° / RT) = -( rH
/ RT) - (P rH
/ RT) - (P rV / RT) + ( rV / RT) + ( rS
/ R) rS
/ R)
Molar volume measurements show that for this exchange reaction  rV
= 0.238 J/bar, thus rV
= 0.238 J/bar, thus
 rH = 52.11 kJ/mol rH = 52.11 kJ/mol
|
The full equation is then
- 52,110 - 19.51*T(K) + 0.238*P(bar) + RT ln K = 0
To plot the K lines in PT space

Net-Transfer Reactions
Net-transfer reactions are those that cause phases to appear or disappear. Geobarometers
are often based on net-transfer reactions because  rV
is large and relatively insensitive to temperature. A popular one is GASP: rV
is large and relatively insensitive to temperature. A popular one is GASP:
|
= Ca3Al2Si3O12 |
+ 2Al2SiO5 |
+ SiO2 |
|
= grossular |
+ kyanite |
+ quartz |
which describes the high-pressure breakdown of anorthite.

For this reaction
 rG = -RT ln [(aqtzaky2agrs)
/ aan3] = -RT ln agrs / aan3 rG = -RT ln [(aqtzaky2agrs)
/ aan3] = -RT ln agrs / aan3
(the activities of quartz and kyanite = 1 because they are pure phases). A best
fit through the experimental data for this reaction by Andrea Koziol and Bob
Newton yields
- P(bar) = 22.80 T(K) - 7317
for  rV = -6.608 J/bar. Again, if we use rV = -6.608 J/bar. Again, if we use
- ln K = -(
 rH / RT)
- (P rH / RT)
- (P rV / RT) + ( rV / RT) + ( rS
/ R) rS
/ R)
and set ln K = 0 to calculate values at equilibrium, we can rewrite the
above as
- (P
 rV / R) = -( rV / R) = -( rH
/ R) + (T rH
/ R) + (T rS / R) rS / R)
or
if T rS / rS /  rV
= 22.8 then rV
= 22.8 then  rS = -150.66 J/mol K rS = -150.66 J/mol K
if  rH / rH /  rV
= 7317 then rV
= 7317 then  rH = -48.357 kJ/mol rH = -48.357 kJ/mol
|
So, we can write the whole shmear as
- 0 = -48,357 + 150.66 T(K) -6.608 P (bar) + RT ln K
Contours of ln K on a PT diagram for GASP look like this:

A Complete Example
Let's suppose you analyze a group of minerals that are in equilibrium and find
the following compositions:
- garnet: Ca0.42Mg0.51Fe2.04Mn0.03Al2Si3O12
- biotite: KMg1.62Fe1.38AlSi3O10(OH)2
- plagioclase:Na0.64Ca0.36Al1.36Si2.64O8
- kyanite
- quartz
Let's determine the equilibrium P and T.
- Determine mole fractions
- Xgrs = 0.14
- Xprp = 0.17
- Xalm = 0.68
- Xann = 0.46
- Xphl = 0.54
- Xan = 0.36
- Determine activities, assuming ideal behavior
- agrs = 0.143 = 0.0027
- aprp = 0.173 = 0.0049
- aalm = 0.683 = 0.31
- aann = 0.463 = 0.097
- aphl = 0.543 = 0.16
- aan = 0.36
- Calculate equilibrium constants:
- KGASP = agrs / aan3 =
0.0025 / 0.363 = 0.054
- KGARB = (aprpaann) / (aalmaphl)
= (0.0049 * 0.097) / (0.31 * 0.16) = 0.0096
- Calculate P and T:
Part 1. Overview of Metamorphism and Tectonics
Part 2. Introduction to Metamorphism
Part 3. Physical Processes of Metamorphism
Part 4. Introductory Phase Equilibria and Thermodynamics
Part 5. Ultramafic Rocks
Part 6. Mafic Rocks
Part 7. Pelitic Rocks
Part 8. Diffusion
Part 9. Thermobarometry
Part 10. Kinetics
Part 11. Interaction Between Metamorphism and Deformation
Part 12. Metamorphism and Geochronology
Part 13. Metamorphism and Tectonics I
Part 14. Metamorphism and Tectonics II
Thermodynamics
Notes
|













 rG =
rG =  VrdP
-
VrdP
-  SrdT
SrdT
 G = 0, such that
G = 0, such that
 rVdP =
rVdP =  rSdT
rSdT
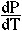 =
= 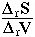
 rV
is small, such that
rV
is small, such that
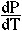 =
= 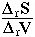
 rG = 0 at equilibrium, we can write
the following approximation (ignoring fluids and variable heat capacities):
rG = 0 at equilibrium, we can write
the following approximation (ignoring fluids and variable heat capacities):
 rG° = -RT ln K
rG° = -RT ln K
 rG°/RT
rG°/RT
 rG°= 0, ln
K = 0 and K = 1. This enables us to write a very important relationship:
rG°= 0, ln
K = 0 and K = 1. This enables us to write a very important relationship:
 rH1,Tref
- T
rH1,Tref
- T rSTref +
rSTref +  rVsP)/
RT
rVsP)/
RT
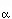 Al2Si3O12,
the activities are
Al2Si3O12,
the activities are
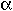 ions,
ions,
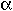 power.
power.
 rV
is large and relatively insensitive to temperature. A popular one is GASP:
rV
is large and relatively insensitive to temperature. A popular one is GASP: