Part 1. Overview of Metamorphism and Tectonics
Part 2. Introduction to Metamorphism
Part 3. Physical Processes of Metamorphism
Part 4. Introductory Phase Equilibria and Thermodynamics
Part 5. Ultramafic Rocks
Part 6. Mafic Rocks
Part 7. Pelitic Rocks
Part 8. Diffusion
Part 9. Thermobarometry
Part 10. Kinetics
Part 11. Interaction Between Metamorphism and Deformation
Part 12. Metamorphism and Geochronology
Part 13. Metamorphism and Tectonics I
Part 14. Metamorphism and Tectonics II
Thermodynamics Notes
Part 4. Introductory Phase Equilibria and Thermodynamics
Read Chapter 2 of An Introduction to Metamorphic Petrology by Bruce Yardley.
or Chapter 24 of Igneous and Metamorphic Petrology by John Winter
or Chapter 18 of Igneous and Metamorphic Petrology by Philpotts
Metamorphic Reactions
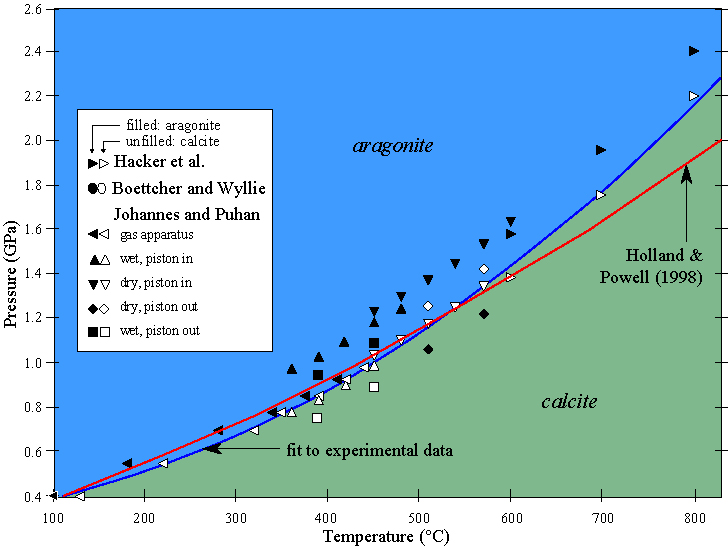
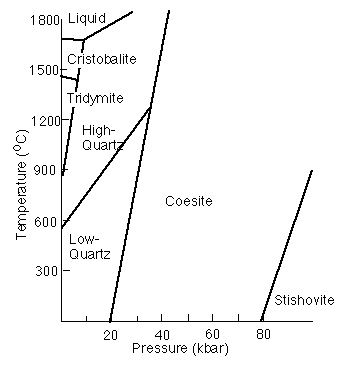
Changes in pressure, temperature, and bulk composition influence which minerals are stable in a given rock. For example, a low-pressure polymorph of CaCO3 is calcite and a high-pressure polymorph is aragonite. One of the ways to establish the P-T conditions over which these two minerals are stable--and the position of the equilibrium boundary (reaction) separating the two is by experiments.
Phase-equilibrium experiments are conducted in experimental apparatus that include diamond anvils, piston cylinders, gas apparatus, and hydrothermal rod-bombs. Here is a diagram of part of a piston-cylinder apparatus:
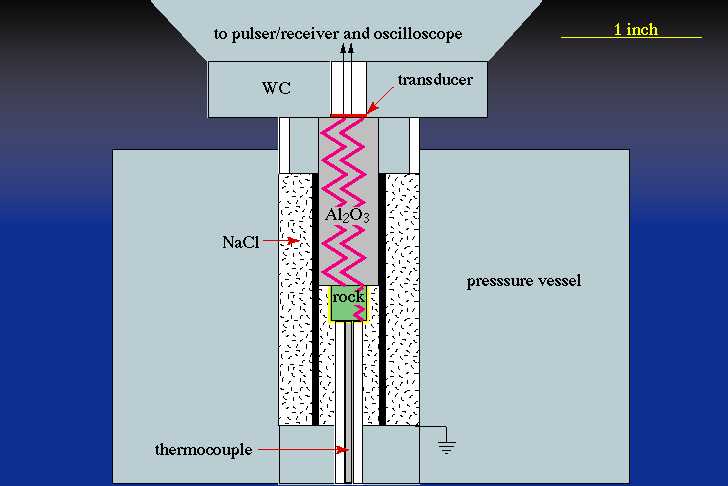
Each experiment is conducted by mixing oxides or minerals in a sealed capsule and then subjecting the capsule to elevated pressure and temperature for periods of time from minutes to months. The products of such experiments look like this back-scattered electron image:

And yield phase diagrams that appear similar to this:
Metamorphic reactions are recognized in the field as isograds, which are mapped surfaces defined by the (dis)appearance of one or more minerals. The Kangmar Dome in Tibet shows a sequence of four prograde isograds surrounding a structurally lower orthogneiss:

Metamorphic Phase Equilibria
system: a rock
phase: a identifiable solid (e.g., plagioclase), liquid (e.g., silicate melt), or vapor (e.g., H2O) in the system
component: a specific chemical constituent of a phase that is useful for understanding thermodynamics or phase equilibria (e.g., for plagioclase, you could use the components ab or an--even though neither may be present as a separate phase).
equilibrium: nothing in the system changes--no further decrease in free energy is possible

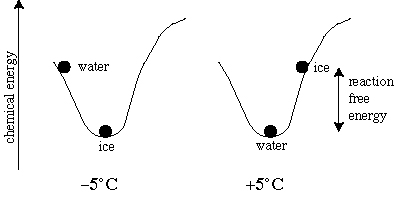
The figure above shows the mechanical analogy for H2O at -5°C and + 5°C and 1 atm. Left: at -5°C, solid H2O has the lowest possible energy state. Right: at +5°C, liquid H2O has the lowest possible energy state. When solid H2O is actually present at +5°C, the difference between the free energy of solid H2O and liquid H2O is available to drive the reaction to form the stable solid H2O phase, and the reaction will go to completion if kinetically possible.
Gibbs Free Energy Change and Reactions
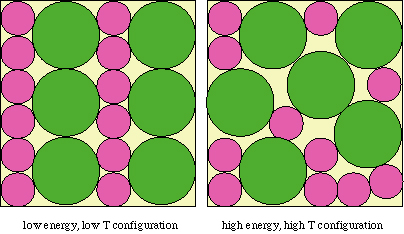
To understand how the energy that is available to drive reactions changes as a function of pressure and temperature within the Earth, we write the (Gibbs) free energy change of a reaction,  rG, as:
rG, as:
where  rH is the enthalpy change of the reaction,
rH is the enthalpy change of the reaction,  rV is the volume change of the reaction, and
rV is the volume change of the reaction, and  rS is the entropy change of the reaction. To calculate whether the change is positive or negative, we calculate the free energy difference between the products and the reactants as "the products minus the reactants". For example, if the Gibbs free energy of solid H2O is 5 kJ/mol and that of liquid H2O is 2 kJ/mol, the Gibbs free energy change of the reaction solid —> liquid,
rS is the entropy change of the reaction. To calculate whether the change is positive or negative, we calculate the free energy difference between the products and the reactants as "the products minus the reactants". For example, if the Gibbs free energy of solid H2O is 5 kJ/mol and that of liquid H2O is 2 kJ/mol, the Gibbs free energy change of the reaction solid —> liquid,  rG, is -3 kJ/mol.
rG, is -3 kJ/mol.
phase: a identifiable solid (e.g., plagioclase), liquid (e.g., silicate melt), or vapor (e.g., H2O) in the system
component: a specific chemical constituent of a phase that is useful for understanding thermodynamics or phase equilibria (e.g., for plagioclase, one could use the components ab or an--even though neither is present as a separate phase).
degrees of freedom: the number of variables (typically P, T, or composition) that can change without changing the number of phases that are stable
phase rule: the utility of the phase rule is to be able to
- specify the number of phases P that exist for given components C at a specific pressure and temperature
- know how many variables such as pressure and temperature may vary for a given set of components and phases
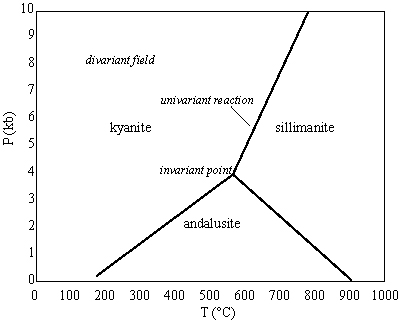
The one-component system H2O or Al2SiO5
If there are 2 degrees of freedom (both P and T can change), the phase rule becomes 2 + P = 1 + 2, and thus P = 1. This means there is a single phase in a divariant field within which P and T can vary and the single phase is still stable
If there is 1 degree of freedom (only P or T can change), 1 + P= 1 + 2, P = 2; there are two phases along a univariant line--a reaction along which P or T can vary and the two phases are still stable
If there are 0 degrees of freedom, 0 + P = 1 + 2, P = 3; there are three phases at an invariant point and if either P or T change the three phases are no longer stable together
Part 1. Overview of Metamorphism and Tectonics
Part 2. Introduction to Metamorphism
Part 3. Physical Processes of Metamorphism
Part 4. Introductory Phase Equilibria and Thermodynamics
Part 5. Ultramafic Rocks
Part 6. Mafic Rocks
Part 7. Pelitic Rocks
Part 8. Diffusion
Part 9. Thermobarometry
Part 10. Kinetics
Part 11. Interaction Between Metamorphism and Deformation
Part 12. Metamorphism and Geochronology
Part 13. Metamorphism and Tectonics I
Part 14. Metamorphism and Tectonics II
Thermodynamics Notes







 rG, as:
rG, as:
 rG =
rG =  rH + P
rH + P rV - T
rV - T rS
rS
 rH is the enthalpy change of the reaction,
rH is the enthalpy change of the reaction,  rV is the volume change of the reaction, and
rV is the volume change of the reaction, and  rS is the entropy change of the reaction. To calculate whether the change is positive or negative, we calculate the free energy difference between the products and the reactants as "the products minus the reactants". For example, if the Gibbs free energy of solid H2O is 5 kJ/mol and that of liquid H2O is 2 kJ/mol, the Gibbs free energy change of the reaction solid —> liquid,
rS is the entropy change of the reaction. To calculate whether the change is positive or negative, we calculate the free energy difference between the products and the reactants as "the products minus the reactants". For example, if the Gibbs free energy of solid H2O is 5 kJ/mol and that of liquid H2O is 2 kJ/mol, the Gibbs free energy change of the reaction solid —> liquid,  rG, is -3 kJ/mol.
rG, is -3 kJ/mol.
 rV term:
rV term:
 rG
rG 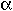 P
P rV
rV
 rV = Vproducts - Vreactants
rV = Vproducts - Vreactants
 rV< 0.
rV< 0.
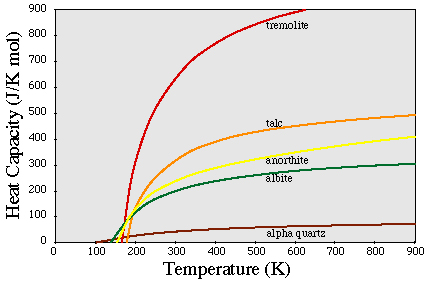
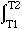 (CP/T) dT
(CP/T) dT
 rG
rG 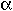 -T
-T rS
rS
 H =
H = 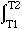 CPdT
CPdT
 rG
rG 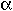
 rH
rH