Part 1. Overview of Metamorphism and Tectonics
Part 2. Introduction to Metamorphism
Part 3. Physical Processes of Metamorphism
Part 4. Introductory Phase Equilibria and Thermodynamics
Part 5. Ultramafic Rocks
Part 6. Mafic Rocks
Part 7. Pelitic Rocks
Part 8. Diffusion
Part 9. Thermobarometry
Part 10. Kinetics
Part 11. Interaction Between Metamorphism and Deformation
Part 12. Metamorphism and Geochronology
Part 13. Metamorphism and Tectonics I
Part 14. Metamorphism and Tectonics II
Thermodynamics Notes
Part 8. Diffusion
Read Chapter 6 of An Introduction to Metamorphic Petrology by Bruce Yardley
or Chapter 30.2.1 of Igneous and Metamorphic Petrology by John Winter
or Chapter 5 of Igneous and Metamorphic Petrology by Philpotts
Diffusion is the transfer of mass via the motion of individual atoms or molecules.
Diffusion within crystals is often discussed in terms of point defects,
which are missing atoms (vacancies) or extra atoms in the crystal
lattice. Every crystal has an equilibrium number of vacancies that
allows the crystal to be in a lower free energy state than if it were
perfect crystal-this is important because it means that crystals are
always "ready to go" when it comes to diffusion.
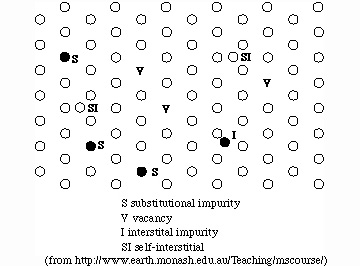
diffusion: mass transfer by the migration of point defects
View diffusion of a single atom (from http://www.earth.monash.edu.au/Teaching/mscourse/)
Diffusive mass transfer takes place in response to chemical
potential gradients. For the purposes of this class, we will simplify
this, and consider diffusion to occur in response to concentration
gradients.
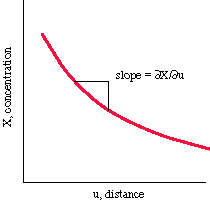
The partial differential 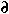 X /
X / 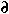 u is used to indicate that the concentration changes as a function of distance.
u is used to indicate that the concentration changes as a function of distance.
If a concentration gradient exists, diffusion will occur until
the concentration is homogeneous. The flux (or rate at which material
passes through a given area) is given by Fick's first law:
- J = -D
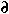 X /
X / 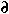 u
u
where D is the diffusivity. In terms of units, this equation is:
- J [atoms m-2 s-1] = -D [m2 s-1]
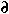 X [atoms m-3]/
X [atoms m-3]/ 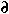 u [m-1]
u [m-1]
(instead of atoms, any other measure of mass can be used, such as moles). For example, if D = 2E-11 m-2 s-1, and the concentration of Mg atoms changes by 0.1 atoms/m3 over a distance of 10 um, the flux of Mg atoms is:
- J = 2E-11 m-2 s-1 * 0.1 atoms/m3 / 10E-6 m = 2E-7 atoms m-2 s-1
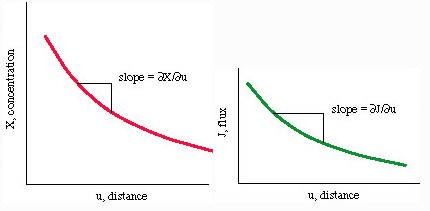
The diffusivity, D, scales with temperature:
- D
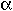 (kT/h) exp(-Q*/RT)
(kT/h) exp(-Q*/RT)
where k is Boltzmann's constant (k = 1.4E-23 J/K), h is Planck's constant (6.6E-34 J/s), and Q* is an activation energy.
When diffusion is occuring, the concentration gradient changes in direct proportion to the gradient in the diffusive flux:
Substituting Fick's first law into this equation yields Fick's second law:
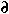 X /
X / 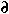 t = D
t = D 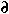 2X /
2X / 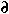 u2
u2
or
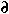 X /
X / 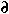 t = D
t = D 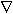 2X, where
2X, where 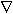 is the del operator and
is the del operator and 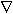 2 is the Laplace operator
2 is the Laplace operator
This equation tells us how fast the composition changes as a result of
the diffusivity and the concentration gradient. For example, a
concentration gradient that begins as a step function decays in the
following manner:
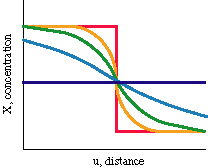
- X = Xo erf [u / 2 (Dt)0.5]
('erf' is a special indefinite integral). Note that this
equation, describing how diffusion changes composition, contains the
characteristic diffusion distance we looked at earlier when discussing
how thermal diffusion changes temperature.
Diffusion Pathways
Different types of diffusion pathways include
- intragranular (volume) diffusion
- grain-boundary film (grain-boundary diffusion)
- bulk fluid
- grain-scale defects

Let's examine three of these processes in more detail:
- Aside from veins, metamorphic rocks have essentially zero porosity,
such that diffusion through bulk fluids is not an important process
except at shallow levels in the crust
- volume diffusion: diffusion within a single grain. Volume diffusion only becomes significant at high temperature.
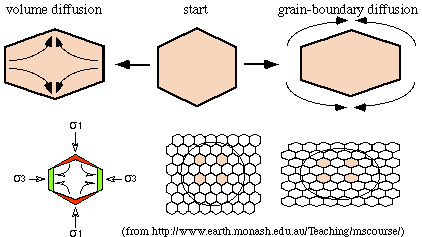
- grain-boundary diffusion: diffusion along a grain
boundary. Grain-boundary diffusion is orders of magnitude faster than
volume diffusion, meaning that grain boundaries are the pathways by
which material is transported through and within rocks of low porosity.

Metamorphic Effects of Diffusion
compositional zoning: Spatial variation in mineral composition
results from slow volume diffusion (diffusion through the mineral
lattice). In garnets, for example, diffusion of the divalent cations is
negligible at low and medium grade, so that the interior of a garnet is
isolated from the rock matrix, and as the P and T change, the garnet
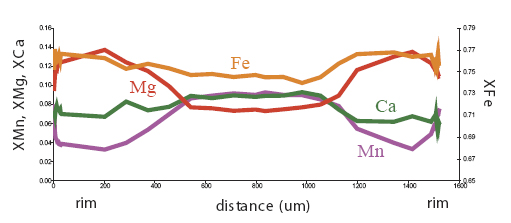
changes composition in response, and develops zoning. Garnets with
prograde growth zoning tend to have Mn and/or Ca-rich cores, with Mg#
increasing steadily toward the rim. Volume diffusion becomes fast
enough at high grade for originally zoned garnets to become
compositionally homogenized.
diffusional/retrograde zoning: zoning in which a pre-existing grain
is modified in composition by exchange of material with the rock
matrix. The usual result in a garnet is a grain with a depletion in Mg,
and commonly also an enrichment in Mn, at the rim. This is found in
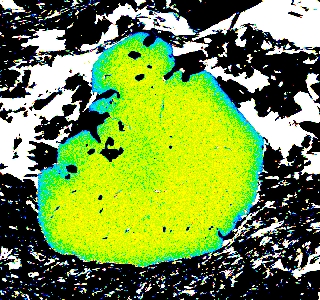
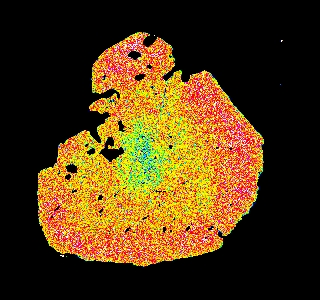
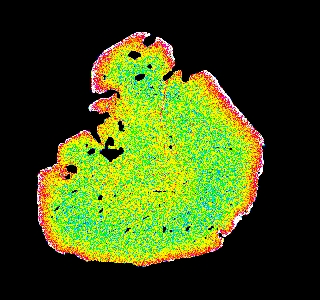
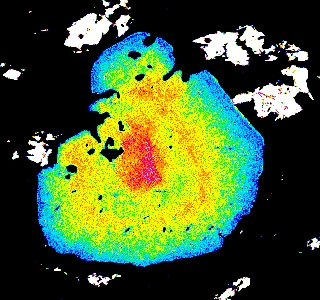
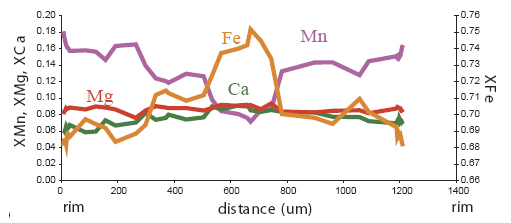
garnets which have experienced temperatures >600°C. Let's look at some examples of garnet zoning. Below are maps of elemental compositions of garnets:
Garnet "0828z8" shows simple prograde zoning, typified by a Mn bell produced by Rayleigh fractionation.
Mg Fe Mn Ca

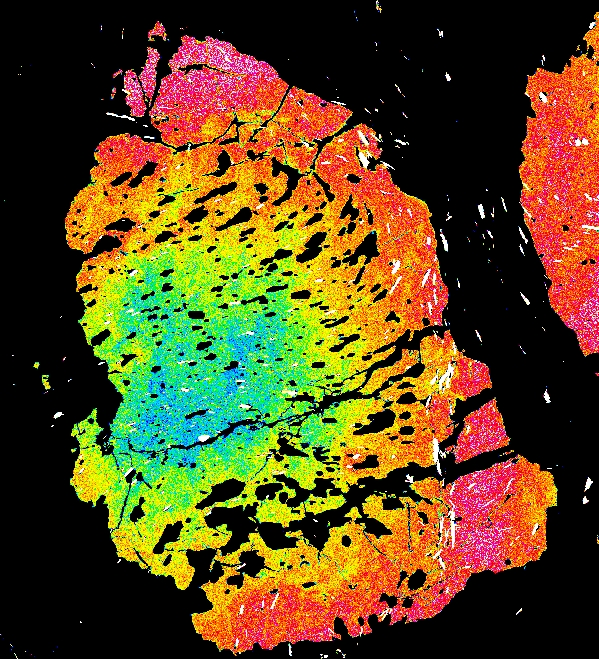
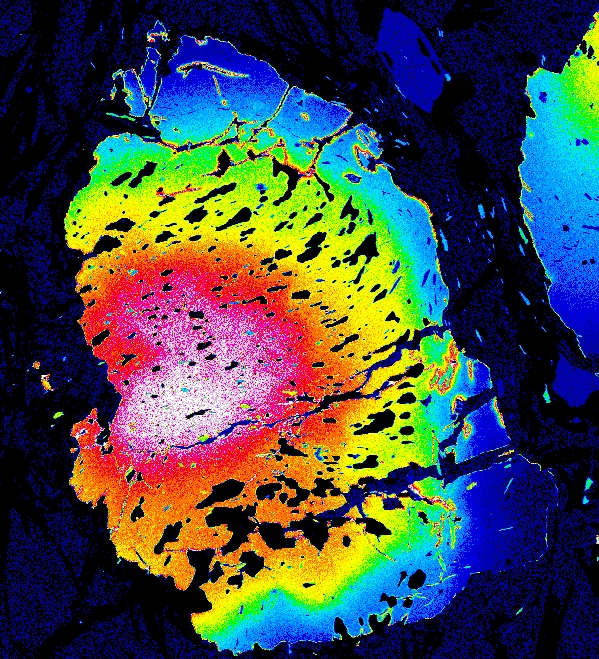

Garnet "0827e3" shows the beginning of resorption, indicated by a Mn kick at the rim where Mn is retained in garnet during resorption.
Mg Fe Mn Ca
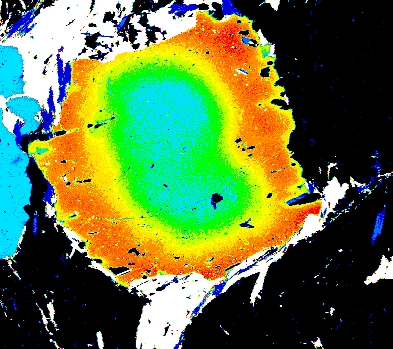
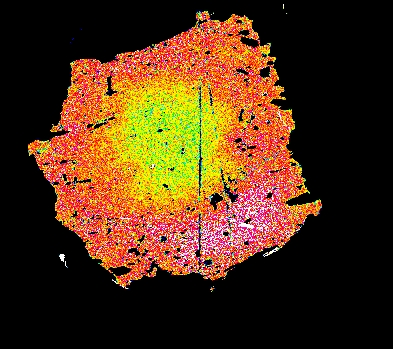
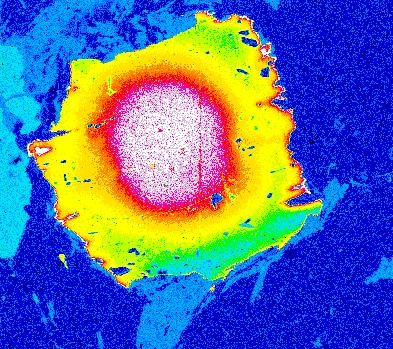

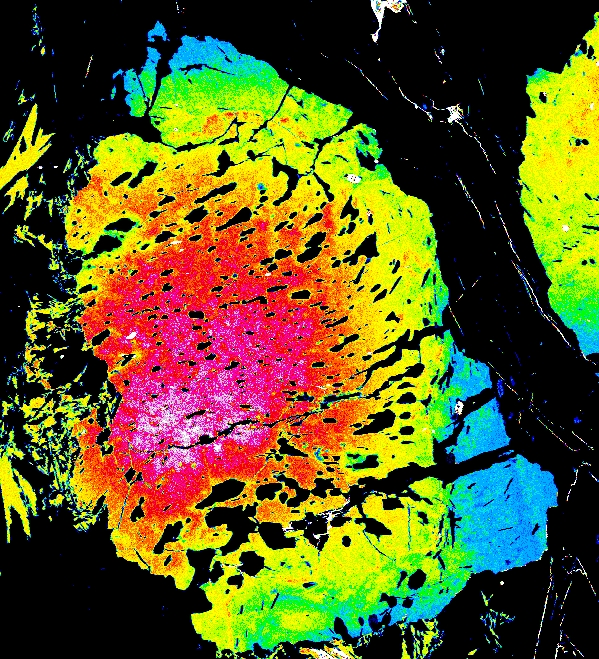
Garnet "0904b2" shows advanced resorption, indicated by Mn migrating toward the core and homogenization of all elements.
Mg Fe Mn Ca
Part 1. Overview of Metamorphism and Tectonics
Part 2. Introduction to Metamorphism
Part 3. Physical Processes of Metamorphism
Part 4. Introductory Phase Equilibria and Thermodynamics
Part 5. Ultramafic Rocks
Part 6. Mafic Rocks
Part 7. Pelitic Rocks
Part 8. Diffusion
Part 9. Thermobarometry
Part 10. Kinetics
Part 11. Interaction Between Metamorphism and Deformation
Part 12. Metamorphism and Geochronology
Part 13. Metamorphism and Tectonics I
Part 14. Metamorphism and Tectonics II
Thermodynamics Notes


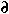 X /
X / 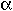 (kT/h) exp(-Q*/RT)
(kT/h) exp(-Q*/RT)

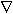 2X, where
2X, where 

















